本文主要讲述如何根据音频信号提取 MFCC 和 FBank 特征,这也是目前在语音识别任务中使用最广泛的两种特征。
人类的语音信号的频率大部分在 10000Hz 以下,根据奈奎斯特采样定理,20000Hz 的采样率就足够了。电话传输的带宽只有 4000Hz,因此电话信号的采样率为 8000Hz,如 Switchboard 语料。我们通常使用麦克风进行音频录制的采样率为 16000Hz,一个采样点使用 16bit 来存储。
下图是特征提取的整个过程,我们现在就按照这流程来讲述一遍。

预加重
在音频录制过程中,高频信号更容易衰减,而像元音等一些因素的发音包含了较多的高频信号的成分,高频信号的丢失,可能会导致音素的共振峰并不明显,使得声学模型对这些音素的建模能力不强。预加重是个一阶高通滤波器,可以提高信号高频部分的能量,给定时域输入信号 $x[n]$,预加重之后信号为: $$ y[n]=x[n]-\alpha x[n-1],\qquad \text{$0.9 \leq \alpha \leq 1.0$} $$
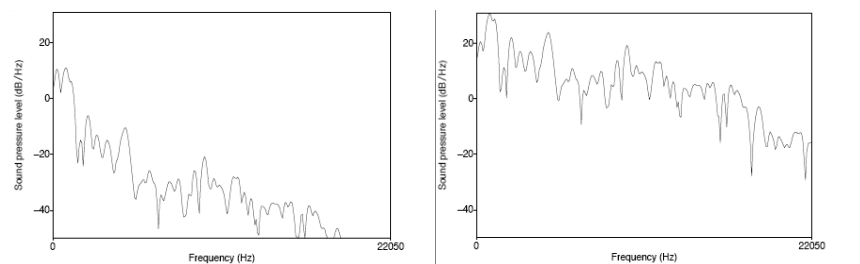
如下图所示,元音音素 /aa/ 原始的频谱图(左)和经过预加重之后的频谱图(右)。
分帧加窗
分帧
语音信号是一个非稳态的、时变的信号。但在 短时间 范围内可以认为语音信号是稳态的、时不变的。这个短时间一般取 10-30ms,因此在进行语音信号处理时,为减少语音信号整体的非稳态、时变的影响,从而对语音信号进行分段处理,其中每一段称为一帧,帧长一般取 25ms。为了使帧与帧之间平滑过渡,保持其连续性,分帧一般采用交叠分段的方法,保证相邻两帧相互重叠一部分。相邻两帧的起始位置的时间差称为帧移,我们一般在使用中帧移取值为 10ms。
对于一个 16000Hz 采样的音频来说,帧长有 16000 * 0.025 = 400 个点,帧移有 16000 * 0.01 = 160 个点。使用 num_samples、frame_len、frame_shift 分别代表 音频的数据点数、帧长和帧移,那么 i 帧的数据需要的点数为$(i-1)*frame\_shift + frame\_len$ ,所以一个有 n 个点的音频,总共能得到 $np.floor((n - frame\_len) / frame\_shift) + 1$ 帧数据。
加窗
因为后面会对信号做 FFT,而 FFT 变换的要求为:信号要么从 -∞ 到 +∞ ,要么为周期信号。现实世界中,不可能采集时间从 -∞ 到 +∞ 的信号,只能是有限时间长度的信号。由于分帧后的信号是非周期的,进行 FFT 变换之后会有频率泄露的问题发生,为了将这个泄漏误差减少到最小程度(注意我说是的减少,而不是消除),我们需要使用加权函数,也叫窗函数。加窗主要是为了使时域信号似乎更好地满足 FFT 处理的周期性要求,减少泄漏。
如下图所示,若周期截断,则 FFT 频谱为单一谱线。若为非周期截断,则频谱出现拖尾,如图中部所示,可以看出泄漏很严重。为了减少泄漏,给信号施加一个窗函数(如图中上部红色曲线所示),原始截断后的信号与这个窗函数相乘之后得到的信号为上面右侧的信号。可以看出,此时,信号的起始时刻和结束时刻幅值都为0,也就是说在这个时间长度内,信号为周期信号,但是只有一个周期。对这个信号做FFT分析,得到的频谱如下部右侧所示。相比较之前未加窗的频谱,可以看出,泄漏已明显改善,但并没有完全消除。因此,窗函数只能减少泄漏,不能消除泄漏。
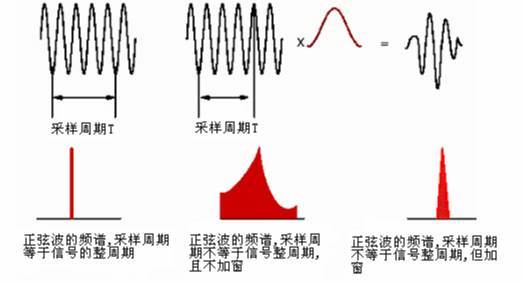
频谱泄露就是分析结果中,出现了本来没有的频率分量。比如说,50Hz 的纯正弦波,本来只有一种频率分量,分析结果却包含了与50Hz频率相近的其它频率分量。
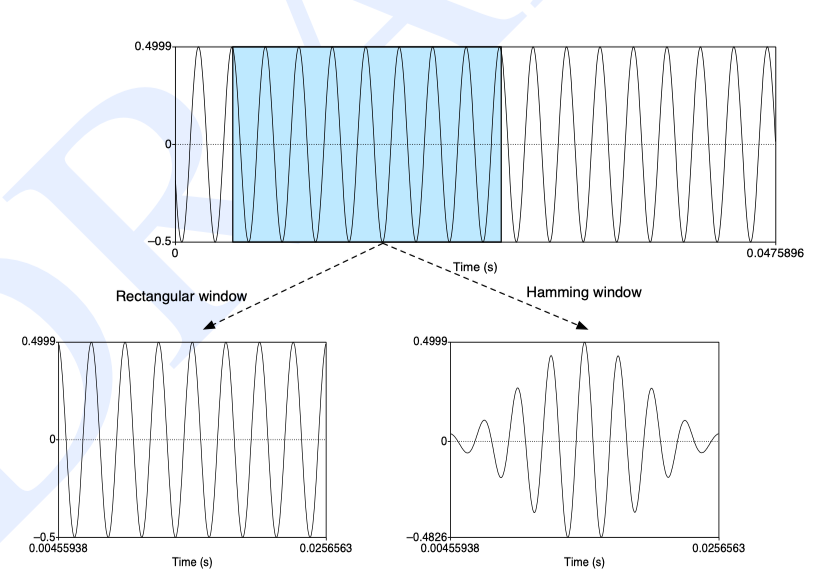
在语音识别中,一般选择汉明窗作为窗函数,它能使信号在窗边界的值近似为 0,从而使得信号趋近于是一个周期信号,该窗函数如下:
$$
w[n] = \begin{cases}
0.54 - 0.46cos(\frac{2\pi n}{L}) & \text{0 $\leq$ n $\leq L - 1$}\
0 & \text{otherwise}
\end{cases}
$$
分别使用矩形窗和汉明窗作用于信号,他们的区别可以从下图中看出来。
DFT
接下来的操作是 离散傅里叶变换(Discrete Fourier Transform,缩写为 DFT),将每个窗口内的数据从时域信号转为频域信号。DFT 的变换公式如下: $$ X(m) = \sum_{n=0}^{N-1} x(n)e^{-j2\pi nm / N} $$ $x(n)$ 是窗口中每个数据点的值,$e$ 是自然底数,$j=\sqrt{-1}$ 。根据欧拉公式,我们可以转换如下的形式: $$ X(m) = \sum_{n=0}^{N-1} x(n) [cos(2\pi nm/N) - jsin(2\pi nm / N)] $$
我们将复指数的形式转换成为了实部和虚部的形式,$X(m)$ 是 DFT 第 m 个输出,$x(n)$ 是输入的时域信号。
首先我们说一下分析频率的概念。假设我们对一个频率为 500 的信号做 16 点的 DFT 变换,那么基础的频率分隔就是 $f_s / N = 500 / 16 = 31.25Hz$,X(m) 所表示的分析频率是 31.25 的整数倍。比如说 X(0) 的分析频率为 0 * 31.25 = 0Hz,X(1) 的分析频率为 1 * 31.25 = 31.25Hz,依次类推,最后的 X(15) 的分析频率为 15 * 31.25 = 468.75Hz。N 点 DFT 的分析频率用该公式表示 $f_{analysis}(m)=mf_s/N$。
在上面的例子中,X(0) 表示的是时域信号中 0Hz DC(direct current) 的幅值,通常我们称 X(0) 的值为直流分量,X(1) 表示的是时域信号中 31.25Hz 的幅值,后面的也是以此类推。
通常 X(m) 包含了两层意思,分别是幅值(magnitude)和功率(power,中文也有成为能量的),下面我们就看看这几个定义在复平面上面的表达。
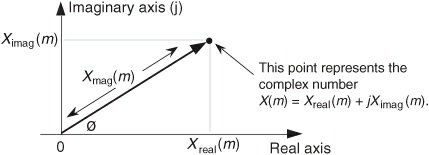
对于任意一个 DFT 的输出 $X(m)$ ,根据它的实部和虚部,写作如下形式: $$ X(m) = X_{real}(m) + jX_{imag}(m) = X_{mag}(m) \quad 角度为X_{\phi}(m) $$ $X(m)$ 的幅值为: $$ X_{mag}(m) = |X(m)| = \sqrt{X_{real}(m)^2 + X_{imag}{}(m)^2} $$ $X(m)$ 的相位角度 $X_{\phi}(m)$ : $$ X_{\phi}(m) = tan^{-1} \left( \frac{X_{imag}(m)}{X_{real}(m)} \right) $$ $X(m)$ 的功率,即功率谱(power spectrum),等于幅值的平方: $$ X_{ps}(m) = X_{mag}(m)^2 = X_{real}(m)^2 + X_{imag}{}(m)^2 $$ 下面让我们对一个包含了 1kHz 和 2kHz 的连续信号进行 8 个点的 DFT,且 2kHz 的相位角为 135°,信号表达如下: $$ x_{in}(t) = sin(2\pi·1000·t) + 0.5 sin(2\pi · 2000 · t + 3\pi/4) $$ 对该连续信号使用 $f_s$ 进行采样,所以每个采样点的时间间隔是 $1/f_s = t_s$ ,有如下表达式: $$ x(n) = x_{in}(nt_s) = sin(2\pi·1000·nt_s) + 0.5 sin(2\pi · 2000 · nt_s + 3\pi/4) $$ 假设我们将采样率设置为 8000Hz,那么这个 8 个采样点的值如下:
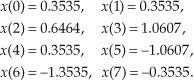
下面我们计算 m = 1 这个 DFT 的输出,$X(1)$ 表示这个 8 个数据点在 1kHz 上面的幅值: $$ X(1) = \sum_{n=0}^{7} x(n) cos(2\pi n/8) - jx(n) sin (2\pi n/8) $$ 计算过程我是直接从《Understanding Digital Signal Processing》书中第三章导出的图片,大家可以从这本书里面看到更多的细节:

从计算结果得知,x(n) 在 1kHz 上面的幅值为 4,功率为 16,相位角度为 -90 度。下面,我将这 8 个点 DFT 的计算结果图片列出来:
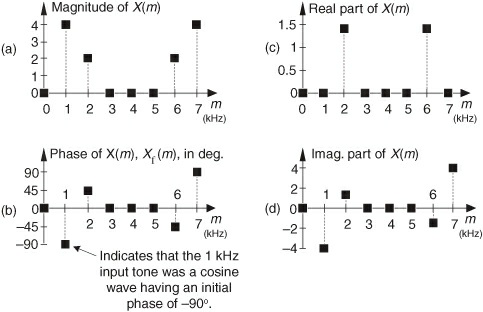
上图中,我们主要关注图(a),可以看到 $X(1)=X(7)$,$X(2)=X(6)$ 等一些频率上面的值是相等的。这个特性称为 DFT 的对称性,对于 $1\le m \le (N/2) -1 $,有 $X(m) = X(n-m)$。由于对称性,如果我们对信号做 512 点 DFT,只需要取前 257 个点(第一个点是直流分量)就行,在语音识别的信号中,一般也是做的 512 点 DFT,然而我们分帧后的一个窗只有 400 个点,这个时候在后面补上 112 个零数据点就行。
从 DFT 的计算公式来看,DFT 的时间复杂度为 $O(n^2)$,在实际中使用的是快速傅里叶变换(Fast Fourier Transform,缩写为 FFT),其时间复杂度是 $O(nlog(n))$,具体的过程大家可以查看 Understanding Digital Signal Processing 书中第四章。
梅尔滤波器组
从 FFT 出来的结果是每个频带上面的幅值,然而人类对不同频率语音有不同的感知能力:对1kHz以下,与频率成线性关系,对1kHz以上,与频率成对数关系。频率越高,感知能力就越差。
梅尔刻度(Mel Scale,其中 Mel 取自单词 melody)是一种非线性刻度单位,表示人耳对音高(pitch)变化的感官,基于频率定义。在 Mel 频域内,人的感知能力为线性关系,如果两段语音的 Mel 频率差两倍,则人在感知上也差两倍。下图则是频率刻度到 Mel 刻度的转换:
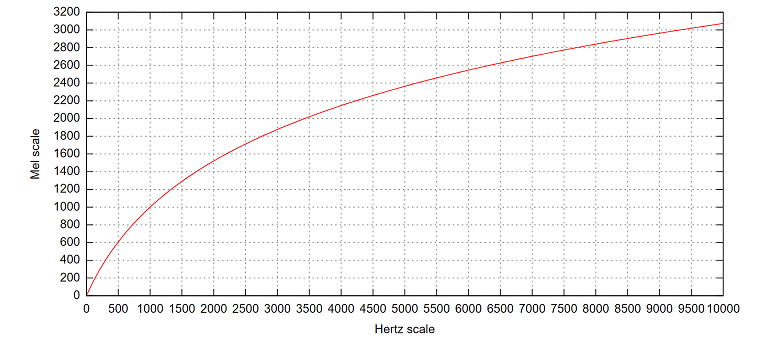
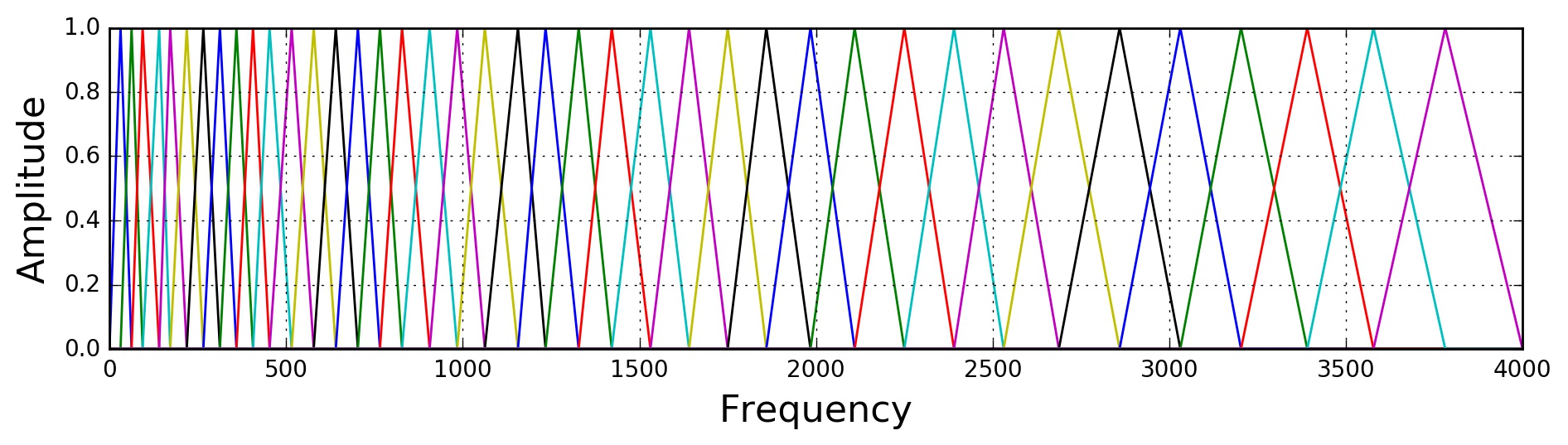
Mel 频率与频率 Hz 转换的公式如下: $$ m = 2595log_{10}(1 + \frac{f}{700}) $$ 下图是 40 个梅尔滤波器在频率轴上面的示意图,要注意的是,上一个滤波器的中间频率是下一个滤波器的开始频率(存在 overlap)。将梅尔域上每个三角滤波器的起始、中间和截止频率转换线性频率域,并对 DFT 之后的谱特征进行滤波,得到 40 个滤波器组能量,再进行 log 操作,就得到了 40 维的 Fbank(Filter Bank)特征。
IDFT
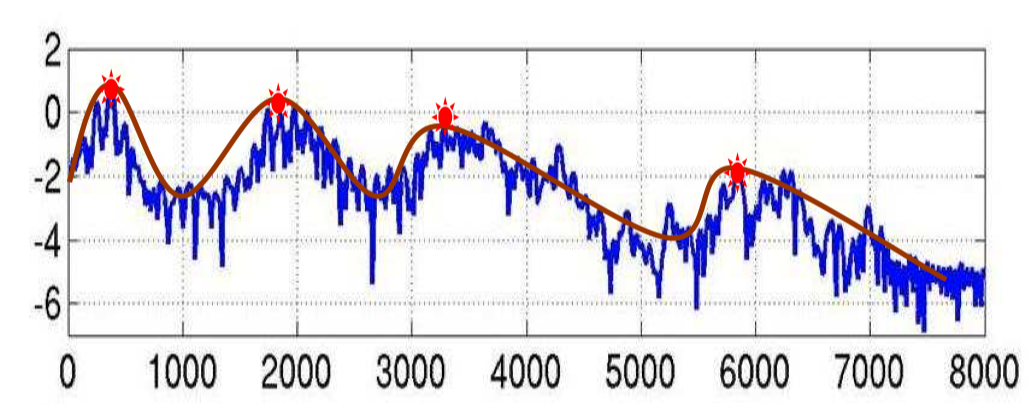
FBank 特征的频谱图大概长下面这个样子,图中四个红点表示的是共振峰,是频谱图的主要频率,在语音识别中,根据共振峰来区分不同的音素(phone),所以我们可以把图中红线表示的特征提取出来就行,移除蓝色的影响部分。其中红色平滑曲线将各个共振峰连接起来,这条红线,称为谱包络(Spectral Envelope),蓝色上下震荡比较多的线条称为谱细节(Spectral details)。
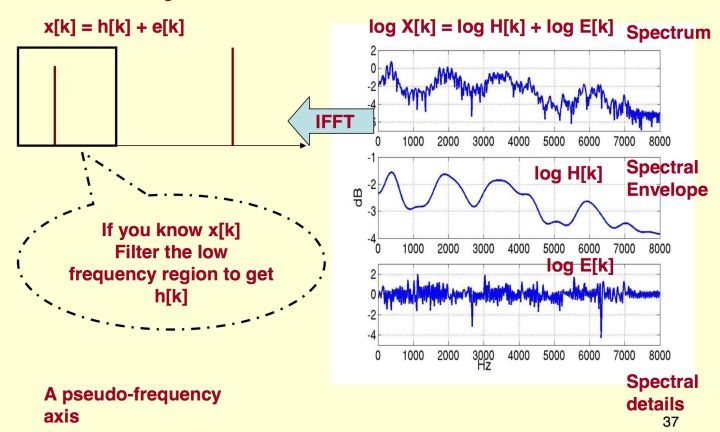
要实现上述操作,需要使用倒谱(Cepstrum)的技术,倒谱的定义是对数谱的谱(spectrum of the log of the spectrum),表示在对数谱上做 DFT,在频谱上面做 DFT 的操作被称为逆离散傅里叶变换(IDFT,Inverse Discrete Fourier Transform)。下面,我们阐述一下生成倒谱系数的原理和流程。
首先,人类发出的声音可以理解为通过声带振动,经过腔体(包括舌头、牙齿等等),形成各种不同的发音。其中声带产生的频谱是很简单的,主要就是腔体的形状和体积等条件决定着各个音素的频谱。所以如果我们知道腔体的形状等信息,就可以准确的对音素进行描述。显然的,腔体的形状对应着上面图中的谱包络,揭示了共振峰的走向。
让我们继续看着这张图,假想横坐标表示的不是频率而是时间,可以发现红线的频率是比较低的,在图里只有 4 个 peak,而蓝色的频率则明显高很多。如果我们对图中的频谱再做一次傅里叶变换,是不是就能将低频率的谱包络和高频率的谱细节给分开呢?答案是肯定可以的。
在频域上,我们假设声带产生振动后的信号为 $E(w)$,然后经过了腔体,这时候腔体可以看成一个滤波器,使用 $H(x)$ 来描述,生成的声音信号为 $X(w)=H(w)·E(w)$ ,我们只关注频谱的能量,忽略相位信息有 $||X(w)||=||H(w)||·||E(w)||$,接下来取对数运算 $log||X(w)||=log||H(w)||+log||E(w)||$,最后作傅里叶逆变换,就可以得到倒谱系数 $IDFT(log||X(w)||)=IDFT(log||H(w)||+log||E(w)||)$。需要注意的是,此处的 IDFT 变换为离散余弦变换(DCT,Discrete Cosine Transform),由于 DCT 具有最优的去相关性的性能,所以倒谱系数之间没有相关性。
该过程可以使用下图来表示,对频谱进行 IDFT 后的域称为 quefrency domain,和时间域类似但不完全一样。在得到频谱的倒谱系数(x[k])后,我们只需要取低位的系数,就可以获得频谱的包络信息。假设我们从 FBank 出来的特征维度是 40 维,那么我们得到的 MFCC(Mel-Frequency Cepstral Coefficients) 系数也是 40 维,这个时候我们再取第 1~k 个系数,输出的就是 k 维的 MFCC。
参考
Topic: Spectrogram, Cepstrum and Mel-Frequency Analysis
Understanding Digital Signal Processing 第三章和第四章
Speech and Language Processing 第九章