语言模型可以说是传统语音识别的三大件(声学模型、语言模型、解码器)之一了,在语音识别的过程中,语言模型用来给定词序列的概率。例如在某次识别中,声学模型模型输出的音节序列为 yu yan mo xing,那么对应的词序列可以为 语言模型 也可以是 语言魔性,这个时候我们就期望通过语言模型来判定 p(语言模型) > p(语言魔性),从而输出 语言模型。 下面我们来看一下这个概率是如何计算的。
如果我们有一个词序列 $ s = (w_1, … , w_n)$,它的概率可以表示为:
$$
\begin{split}
p(s) &= p(w_1, w_2, w_3, …, w_n) \
&= p(w_1^n) \
&= p(w_1)p(w_2|w_1)p(w_3|w_1^2)…p(w^n|w_1^{n-1}) \
&= \prod_{k=1}^n p(w^k|w_1^{k-1}) \
\end{split}
$$
那么 $p(w_1), p(w_2|w_1), p(w_3|w_1^2)…p(w^n|w_1^{n-1})$ 这些概率是怎么来的呢?是从语料里面通过计数算出来的,比如有句话 my personal website is asr dot pub,那么有:
$$
p(pub\ |\ my\ personal\ website\ is\ asr\ dot) = \frac {c(my\ personal\ website\ is\ asr\ dot\ pub)}{c(my\ personal\ website\ is\ asr\ dot)}
$$
c(a b) 表示 a b 序列在语料中出现的次数。 从这个计算公式我们可以看到一个缺点,就是当历史信息过长的时候,可能语料库里面没有完全一致的序列存在,随着历史信息的增加,数据稀疏的问题会比较显著,一个容易想到的做法是使用几个最近的历史词来代替整个历史词序列,这就引出了下一个话题:n-gram 语言模型。
n-gram 语言模型与评价方法
n-gram 是指使用前 n-1 个词来估计当前(第 n 个)词,即 $p(w_i|w_1^{i-1})=p(w_i|w_{i-n+1}^{i-1})$。根据 n-gram 中 n 的值,我们有 unigram($p(w_i)$)、bigram($p(w_i|w_{i-1})$)、trigram($p(w_i|w_{i-2}^{i-1})$) 等等。n-gram 中概率的计算方法也是通过计数来得到的,只不过和上面说的一样,也会有语料中不存在词序列,关于这个问题的解决方法我们在后面的平滑算法中提出来。
在我们训练好一个语言模型后,我们可以用这个语言模型对测试文本进行测试,在测试文本上面得到的概率值越大越好。困惑度(Perplexity)就是衡量语言模型性能的一个算法,假如我们有一个句子 $W=w_1,w_2,w_3,…,w_n$ ,具体计算公式如下所示:
$$
\begin{split}
PP(W) &= P(w_1w_2…w_n)^{-\frac {1}{n}} \
&= \sqrt[n]{\frac{1}{p(w_1w_2…w_n)}} \
&= \sqrt[n]{\prod_{i=1}^{n} \frac{1}{p(w_i|w_{i-n+1}^{i-1})}}
\end{split}
$$
从公式可以看出,语言模型性能越好,那么困惑度就越低。下面的数值来自 Dan Jurafsky 的教学文档,链接见参考文章:
- WSJ 数据集,训练集有 38 million 词,测试集有 1.5 million 词

因为不同的词出现在句首或者句尾的概率是不同的,比如像语气词 吗 啊 嘛 在句尾就经常出现。所以我们在训练语料中每一行文本句首加上 <s> ,句尾加上 </s>,用来标识一句话开始和结束,这样训练好输出的语言模型就可以知道不同的词出现在句首和句尾的概率了。而且在训练语言模型的时候,我们也不会用到训练语料里面所有的词,我们会提供一个词表,语料里面不在词表中的词会被标记成 <unk>。
平滑算法
正如我们上面所说的,由于训练语料的稀疏性,有些词序列找不到怎么办?使用平滑的方法来解决,核心思想是 将看见的事件概率量的一部分分配给未看见的事件,用老话讲就是劫富济贫了。
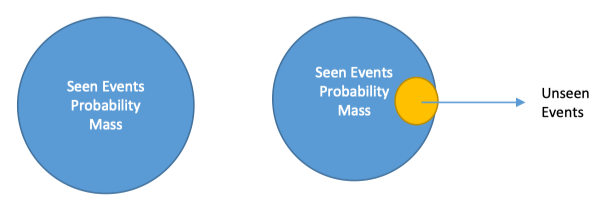
拉普拉斯平滑
拉普拉斯平滑(Laplace Smoothing)也称为 Add-one Smoothing,其核心思想是 将每个计数加一,从而使得任何词序列都有计数。以 bigram 为例,常规操作是 $P_{MLE}(w_i|w_{i-1}) = \frac {c(w_{i-1}w_i)}{c(w_i)}$,拉普拉斯平滑为 $P_{laplace}(w_i|w_{i-1}) = \frac {c(w_{i-1}w_i) + 1}{c(w_i)+V}$,$V$ 是词表中词的个数。为了简单的举个例子,假设我们的训练语料有且只有一条文本:
# 词表大小为 7
my personal website is asr dot pub
那么 $P_{MLE}(personal\ |\ my) = \frac {1}{1} = 1$,$P_{laplace}(personal\ |\ my) = \frac {1+1}{1+7} = \frac {2}{8}$,通过拉普拉斯平滑,原本不存在的词序列也会得到一个概率了,比如 $P_{laplace}(website\ |\ my) = \frac {0+1}{1+7} = \frac {1}{8}$。从这个例子中,我们可以看到,拉普拉斯平滑会将原本一个比较大的概率,削减成一个比较小的值,所以拉普拉斯一般不用在平滑算法中。
在这里我们要引入两个比较重要的概念,在后面的平滑算法中会经常碰到,分别是 调整计数(adjusted count) 和 打折率(discount
ratio)。以 unigram 为例,我们将 $w_i$ 的计数记为 $c_i$,$P_{MLP}(w_i)=\frac{c_i}{N}$,$P_{laplace}(w_i)=\frac{c_i + 1}{N+V}$。调整计数的意义是描述平滑算法仅对 $P_{MLP}(w_i)$ 中分子的影响,所以我们需要将 $P_{MLP}$ 与 $P_{laplace}$ 中的分母先统一一下:
$$
\begin{split}
P_{laplace}(w_i) &= \frac{C_i + 1}{N+V} \
&= \frac{\frac{(C_i + 1)*N}{N+V}}{N} \
\end{split}
$$
如上所示,$w_i$ 的计数由 $c_i$ 变成了 $\frac {(c_i + 1)*N}{N+V}$,所以调整计数为 $c^* = \frac {(c_i + 1)*N}{N+V}$,打折率 $d_c = \frac{c^*}{c_i}$,从公式可以看出打折率的意义是调整计数与原计数的比率 。
古德图灵平滑
古德图灵平滑(Good-turing Smoothing),思想是 用你看见过一次的事情(Seen Once)估计你未看见的事件(Unseen Events),并依次类推。
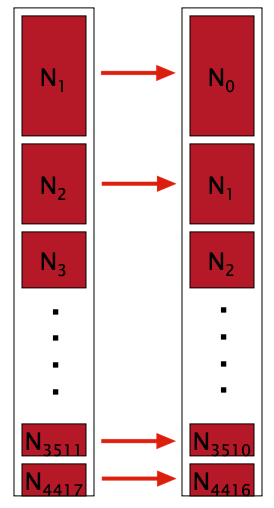
我们定义 $N_c$ 表示频率 c 出现的频数(Frequency of frequency c),这里借用 Dan Jurafsky 的例子如下:
# 一条文本
Sam I am I am Sam I do not eat
# 每个词出现的频率
I 3
sam 2
am 2
do 1
not 1
eat 1
# 各个频率的频数
N1 = 3
N2 = 2
N3 = 1
根据上面讲的,我们得出调整计数 $c^*=\frac{N_{c+1}*(c+1)}{N_c}$。所有词表上在语料中没有出现的词的概率为 $P^*_{GT}(Unseen Events) = \frac{N_1}{N}$,这个值也被称为遗漏量(missing mass),如果我们要求单个未出现词的概率,则为 $P^*_{GT}(Unseen Events) = \frac{N_1}{N*N_0}$,其中 $N_0$ 是所有未出现词的个数。
该平滑算法不会单独使用,一般与其他平滑算法结合起来使用。
Jelinek–Mercer 平滑
假设我们的语料中,$C(BURNISH\ \ THE) = 0$ 和 $C(BURNISH\ \ THOU) = 0$ ,那么根据拉普拉斯和古德图灵平滑算法,我们有 $P(THE|BURNISH) = P(THOU|BURNISH)$,但是这个结论似乎与我们的直觉相反,因为 THE 出现的频率要远大于 THOU,更符合现实规律的是 $P(THE|BURNISH) > P(THOU|BURNISH)$。
我们可以将 bigram 和 unigram 的概率进行插值达到我们所需要的结论,插值如下: $$ P_{MLE}(w_i|w_{i-1}) = \lambda P_{MLE}(w_i|w_{i-1}) + (1-\lambda)P_{MLE}(w_i) $$ 该方法是由 Jelinek and Mercer (1980) 提出来的,目前使用的一个版本是由 Brown, S. A. Della Pietra, V. J. Della Pietra, Lai and Mercer (1992a) 发表的: $$ P_{interp}(w_i|w_{i-N+1}^{i-1}) = \lambda_{i-N+1}^{i-1}P_{MLE}(w_i|w_{i-N+1}^{i-1}) + (1-\lambda_{i-N+1}^{i-1})P_{interp}(w_i|w_{i-N+2}^{i-1}) $$ 可以看出来这是一个递归的计算公式,那么要终止这个递归公式有两种方法:
- 使用 unigram 的 MLE 概率,或者其他的平滑概率
- 使用 zero-gram 的概率,也称为 uniform model,其值为 $P_{w_i}=\frac{1}{|V|}$,$|V|$ 是词表的大小
计算公式中的 $\lambda$ 可以在 held-out set 上面用 EM 算法迭代出来,一般不会为每个 $w_{i-N+1}^{i-1}$ 计算一个单独的 $\lambda_{i-N+1}^{i-1}$,然而设置一个全局的 $\lambda_{i-N+1}^{i-1}$ 会导致一个比较差的性能。通常的做法是根据 $C(w_{i-N+1}^{i-1})$ 的值,将 $\lambda_{i-N+1}^{i-1}$ 放入不同的 bucket,相同的 bucket 里面的 $\lambda_{i-N+1}^{i-1}$ 的值都是一样的,该方法的论文为 A Maximum Likelihood Approach to Continuous Speech Recognition 。
Witten-Bell 平滑
Witten–Bell 平滑开出出来的初衷是用于文本压缩的,可以认为它是 Jelinek–Mercer 平滑的一个特例。它的计算公式和上面的 Jelinek–Mercer 递归插值是一样的,只不过 WB 平滑在计算 $\lambda_{i-N+1}^{i-1}$ 时有它自己的方法。我们需要定义 $w_{i-N+1}^{i-1}$ 后面跟着的词的种类数,用符号 $N_{1+}(w_{i-N+1}^{i-1}·)$ 来表示,其正式的定义为: $$ N_{1+}(w_{i-N+1}^{i-1}•) = |{ w_i:C(w_{i-N+1}^{i-1} w_i) > 0 }| $$ $N_{1+}$ 表示出现过一次以上的词序列种类数,• 表示任意的词都会被统计到。我们对 WB 平滑算法中的 $\lambda_{i-N+1}^{i-1}$ 赋值如下: $$ 1-\lambda_{i-N+1}^{i-1} = \frac {N_{1+}(w_{i-N+1}^{i-1}•)} { N_{1+}(w_{i-N+1}^{i-1}•) + \sum_{w_i} C(w_{i-N+1}^{i}) } $$ 所以我们带入上面 Jelinek–Mercer 递归公式中有: $$ P_{WB}(w_i|w_{i-N+1}^{i-1}) = \frac { C(w_{i-N+1}^{i}) + N_{1+}(w_{i-N+1}^{i-1}•) P_{WB}(w_i|w_{i-N+2}^{i-1})} { N_{1+}(w_{i-N+1}^{i-1}•) + \sum_{w_i} C(w_{i-N+1}^{i}) } $$
卡茨平滑
卡茨平滑(Katz Smoothing),其思想是 若 n 阶语言模型概率存在,则直接使用打折后(一般使用 Good-turing 打折算法)的概率,否则将打折省出的遗漏量分配给 n-1 阶的的语言模型概率,依此类推。
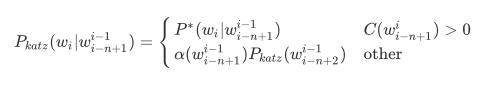
$\alpha(w_{i-n+1}^{i-1})$ 被称为归一化因子,也就是训练好的语言模型 arpa 文件中最后一列回退概率。
$$
\alpha(w_{i-n+1}^{i-1}) = \frac {1-\sum_{w_i:c(w_{i-n+1}^{i})>0}P_{GT}^*(w_i|w_{i-n+1}^{i-1})}
{1-\sum_{w_i:c(w_{i-n+1}^{i})>0}P_{GT}^*(w_i|w_{i-n+2}^{i-1})}
$$
$w_i:C(w_{i-n+1}^{i})$ 所表达的意义为:词序列 $w^{i-1}_{i-N+1}$ 是固定的, $w_i$ 是任意的。
下面让我们看下 $\alpha(w_{i-n+1}^{i-1})$ 是如何推导出来的:

克奈瑟-内平滑
Church 和 Gale(1991)对具有 2200 万词的 AP Newswire 语料进行 Good-turing 打折计算后得到如下表格:
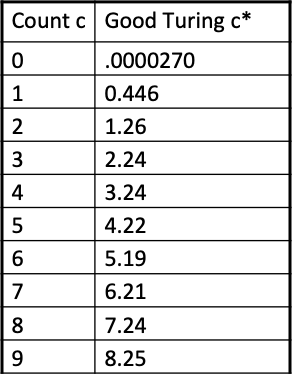
除了 0 和 1 之外,其他的打折计数近似于原计数减去 0.75(使用 D 表示),这样在计算中就比较快了。在实际应用中,0 和 1 会有专门的处理。绝对打折(Absolute Discounting)公式如下所示:
$$
P_{AbsoluteDiscounting}(w_i|w_{i-1}) = \frac{C(w_{i-1}w_i)-D}{C(w_{i-1})} + \alpha(w_{i-1})P(w_i)
$$
$\alpha(w_{i-1})$ 是归一化因子,即打折后概率的遗漏量,$\alpha(w_{i-1}) = \frac{D}{C(w_{i-1})}|C(w_{i-1}w_i)>0|$,$P(w_i)$ 是 unigram 的概率。但是在 Kneser-Ney 中用的不是普通的 unigram 概率,而是一种称为接续(Continuation)概率的 unigram。我们举一个 Dan Jurafsky 的例子,我们现在训练好了一个 bigram 的语言模型,然后需要对一个句子进行预测其中的词,I can't see without my reading ____,从 unigram 的角度来说,Francisco 的概率要大于 glasses,但是 Francisco 往往在 San 的后面。所以我们定义接续概率:对于一个词,如果在训练文本中有更多的上下文组合,那么它应该就有更高的概率,其数学公式定义如下:
$$
P_{continuation} = \frac {| {w_{i-1}:C(w_{i-1}w_i)} > 0 |} {\sum_{w_i} |w_{i-1}:C(w_{i-1}w_i)>0| }
$$
所以有 Kneser-Ney 平滑算法的具体公式为:
$$
P_{KN}(w_i|w_{i-N+1}^{i-1}) = \frac{max(C(w_{i-N+1}^{i})-D,0)}{C(w_{i-N+1}^{i-1})} + \alpha(w_{i-N+1}^{i-1})P_{KN}(w_i|w_{i-N+2}^{i-1})
$$
参考文章
Introduction to N-grams — [ NLP || Dan Jurafsky || Stanford University ]
Lecture 18 — Good Turing Smoothing — [ NLP || Dan Jurafsky || Stanford University ]
All Our N-gram are Belong to You
An empirical study of smoothing techniques for language modeling
4. Part 3: Implement Witten-Bell smoothing
A Maximum Likelihood Approach to Continuous Speech Recognition